
题目来源:洛谷P1150 Peter 的烟
题目描述
Peter 有 n 根烟,他每吸完一根烟就把烟蒂保存起来,k(k>1)个烟蒂可以换一个新的烟,那么 Peter 最终能吸到多少根烟呢?
与某些脑筋急转弯不同的是,Peter 并不能从异次元借到烟蒂,抽完后再还回去。
感觉传统香烟还是不如电子烟吧(电子烟没有烟蒂)
输入格式
每组测试数据一行包括两个整数 n,k(1<n,k≤108)。
输出格式
对于每组测试数据,输出一行包括一个整数表示最终烟的根数。
思路
- 先以样例2为例,
n = 10, k = 3时
第一次抽,抽了10根, 剩下10个烟蒂可以兑换3根烟,还剩1个
第二次,抽了3根,剩下的3+1个烟蒂可以兑换一根烟,还剩1个
第三次,抽了1根,烟蒂只剩1+1<3,无法兑换,抽烟终止
- 这样,我们能梳理这一题目的逻辑:
除第一次外,每次先抽完上次兑换的烟,剩下的烟蒂加上之前剩下的烟蒂,尝试兑换
如果能够兑换(yandi >= k),继续循环;反之退出。
int smoking(int n,int k){
//初始化部分
int num = n; // 先吸完初始的 n 根烟
int yandi = n; // 产生 n 个烟蒂
//循环部分
while(yandi >= k){
int newSmoke = yandi / k; // k 个烟蒂换 1 根新烟
num += newSmoke; // 吸掉新换来的烟
yandi = yandi % k + newSmoke; // 剩余烟蒂 = 换不了的 + 新烟吸完的
}
return num;
}
//一个更简单的实现
int smoking(int n,int k){
static int sum = n;//静态变量,只初始化一次
do{
sum = sum + n / k;
n = n % k + n / k;
} while (n >= k);
}用while循环很好实现,那么,我们要想用更少的代码实现,应该怎么办呢?
使用递归。
递归的定义
借着这个问题,我们先了解一下递归。
递归的基本思想是某个函数直接或者间接地调用自身。
递归,拆开来看,是”递“和”归“的两个过程。
类比我们搜索信息的过程,递归的过程就是一个不断追问,理解意思(到达终止条件)后回到文中的过程。
举个例子,这是算法组学长授课的一张图

注意右下角,当我们要找”U群常见问题速查“的图片时,我们进入”U群常见问题速查“,又发现了这个问题,再进入”U群常见问题速查“,再发现这个问题……
这就是一种无限递归。
还没太搞懂?我们来看一下下面的实际应用。
递归的实际应用
实际问题中,我们一般采用有限次数的递归。
- 一个典型的例子就是阶乘的递归实现
int fact(int n)//输入为自然数
{
return n == 0 ? 1 : n * f(n-1);//这里使用了三目运算符,注意 == 0不能舍去
}以n = 4的情况为例,输入4后函数作出如下操作:
4 == 0 为假,因此返回 4 * f(3)
f(3)返回值为多少?我们进入f(3),3 == 0仍然为假,返回 3 * f(2)
f(2)又返回多少?返回2* f(1)
f(1)呢?返回1 * f(0).
到f(0)时,我们终于得知了返回值为1
这便是”递“。
因此
f(1) = 1 * f(0) = 1;
f(2) = 2 * f(1) = 2;
f(3) = 3 * f(2) = 6;
f(4) = 4 * f(3) = 24;
这便是”归“。
《算法竞赛入门经典中》有一个有趣的比喻:
皇帝(拥有main函数的栈帧):大臣,你给我算一下f(3)。
大臣(拥有f(3)的栈帧):知府,你给我算一下f(2)。
知府(拥有f(2)的栈帧):县令,你给我算一下f(1)。
县令(拥有f(1)的栈帧):师爷,你给我算一下f(0)。
师爷(拥有f(0)的栈帧):回老爷,f(0)=1。
县令:(心算f(1)=f(0)*1=1)回知府大人,f(1)=1。
知府:(心算f(2)=f(1)*2=2)回大人,f(2)=2。
大臣:(心算f(3)=f(2)*3=6)回皇上,f(3)=6。
皇帝满意了。
这或许能部分说明递归的本质。
- 另一个例子是最大公因数(gcd)的计算
int gcd(int a,int b){
return b ? a : gcd(b,a % b);
}这里采用的是欧几里得算法(辗转相除法)
- 先介绍一下实现原理:gcd(a,b) = gcd(b,a % b)
举个例子,18和12的最大公因数显然是6,6即为18和12的余数。所以gcd(18,12)=gcd(12,6)
数学原理:设 a % b = r1,那么a = n1 * b + r1;
下一轮,输入的值是b和a % b(r1);
设b % r1 = r2,则 b = n2 * r1 + r2;
下一轮,输入的值是a % b(r1)和b % r1(r2);
设r1 % r2 = r3,则 r1 = n3 * r2 + r3;
(此时a = (n1 * n2 + 1) * r1 + n1 * r2 = (n1 * n2 + 1) * (n3 * r2 + r3) + n1 * r2)
……
通过数学归纳法可以知道,之后输入的数值都可以转换成rn和r(n+1)的形式表示,这样当rn和r(n+1)存在倍数关系时,就会到达终止条件。
直观地看,实现过程如下图:
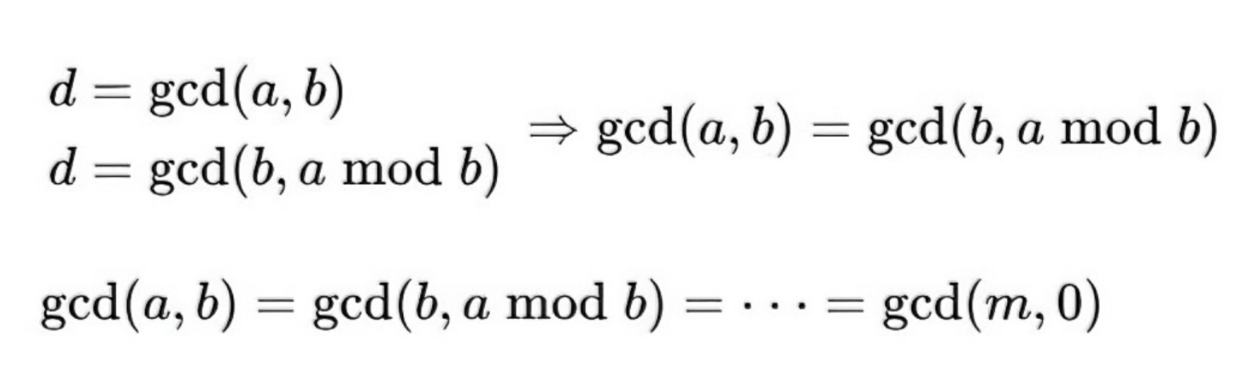
- 有读者可能会担心递归的时间复杂度问题,实际上,递归的时间复杂度一般为O(n)或O(logn),如果实现正确不会出现明显的运行时间延长
回到本题,如何用递归实现?
让我们回到本体的变量间核心关系上。
对上面的代码等价替换变量可以发现这个表达式:n = n / k + n % k
- 如何解释这个式子?
按照之前的思路,我们每次计算好的应该是本轮抽的烟数目,将烟蒂(n/k+n%k)交给下一轮处理,直到最后一轮烟蒂不够换烟
但是,要想实现代码的简洁性,我们应该只有两个变量,k值固定,那么只能每次传输一个参数
但是这一次需要换一种思路:由于剩下的烟蒂无法存储(“n”只能用于传输烟蒂数量),我们每轮只能抽能兑换烟部分(能被k整除)的烟数,剩下的放到下一回合再抽。
因此n / k是烟蒂兑换的烟数量,而 n % k则是剩下的烟(留着换完抽)的数量,n就表示烟的数量,这个表达式就是烟数量的变化过程。
这样一来,传入和返回的n的定义就相同了(都可以看成上一轮留下的烟数量)
同时,根据题目意思,函数内部要进行的就是这一轮抽的烟数,可以用n / k * k或n - n % k表示
int smoking(int n,int k)
{
if(n < k)
return n;
return n / k * k + smoking(n / k + n % k, k);//return已经退出函数,无需else
}简化成一行就是
int smoking(int n,int k){
return n < k ? n : (n / k) * k + smoking(n / k + n % k, k);
}在这个程序中,当传入的n >= k时,我们会抽掉能被k整除的部分,并把剩余的烟和兑换的烟给下一个递归进程处理,当最后n < k时,程序会返回n(抽掉所有烟)。这个过程中,所有被抽掉的烟都在每一个进程中被加上,最后返回主进程的就是抽过的烟数。
完整程序如下:
#include <bits/stdc++.h>
using namespace std;
int smoking(int n,int k){
return n < k ? n : (n / k) * k + smoking(n / k + n % k, k);
}
int main(){
int n,k;
cin >> n >> k;
cout << smoking(n,k) << endl;
return 0;
}最后对比一下直觉和递归的不同之处:
| 直觉 | 递归 | |
|---|---|---|
| 抽烟数量 | 每次全抽 | 只抽k的整数倍根 |
| 参数数量 | 多个 | 每次只传递一个 |
| 烟蒂保存 | 用参数保存(可保存多个回合) | 只保存到下一回合 |
所以说:
简洁而严密,这就是递归定义的优点。
当然,递归肯定有它本身的缺陷,它的特性导致它难以阅读且在大型项目中容易出错
递归深度过大会导致栈溢出(Stack Overflow),应谨慎使用。
如图,在计算阶乘时,如果输入f(100),程序直接返回了错误结果0
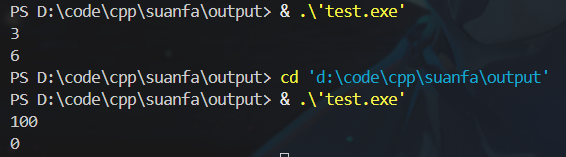
- 在搜索时,还发现了一种时间复杂度为O(1)的数论解法,贴在这里,想了解原理的可以去原文章:
#include <iostream>
using namespace std;
int main() {
int n, k;
cin >> n >> k;
cout << n + (n - 1) / (k - 1) << endl;
return 0;
}结语
递归是一种简洁高效的小规模程序实现方式,适合学习算法时锻炼脑力,但不适合大规模的项目开发。
此外,在本章中笔者未涉及到递归的原理,有兴趣的读者可以自行查询